MC: Februar ’20

• • Der Lösungsvorschlag (Bilddatei, PDF- oder Word-Datei mit Namen und Klasse versehen an kom@gymgmunden.at) muss fristgerecht (Zeitstempel des EMails) eingereicht werden.
  • Die Aufgabe muss ohne Technologieeinsatz gelöst und nachvollziehbar dokumentiert werden.
  • Bei mehreren richtigen Lösungen folgt eine Reihung nach Zeitpunkt des Einlangens.
  • Pro Runde darf nur ein Lösungsversuch eingereicht werden.
  • Die Teilnehmerin/der Teilnehmer ist damit einverstanden, dass ihr/sein Lösungsvorschlag ggf. auf der Mathemator-Seite veröffentlicht wird.
  • Der Gewinnerin/dem Gewinner winkt eine würdevolle Ehrung durch den Mathemator!
  • Die Mathe-Challenge findet monatlich statt.
  • Unterstufenschüler/innen sind auch an der Oberstufen-Mathe-Challenge teilnahmeberechtigt.

Aus einer vorgegebenen Anzahl an Streichhölzern werden durch Aneinanderlegen der Streichhölzer auf einem Tisch Figuren gebildet. Dabei stellt sich die folgende Frage:

Wie viele sich topologisch unterscheidende Figuren können (in einer Ebene, also auf dem Tisch) aus der gegebenen Anzahl an Streichhölzern gebildet werden?

Nun zu den Spielregeln:

Zwei geometrische Figuren sind topologisch gleich (äquivalent), wenn sich die eine Figur aus der anderen bilden lässt (und umgekehrt), ohne die Figur dabei zu zerschneiden (beim Verschieben eines Streichholzendes entlang eines anderen Streichholzes darf der Kontakt nicht unterbrochen werden; Streichhölzer dürfen nicht gebrochen werden) und ohne zu kleben (freie Streichholzenden bleiben auch nach der Umformung frei). Das Drehen/Kippen von freien Streichholzenden um einen Knoten (siehe linke Abbildung im Beispiel 1) ist erlaubt. Die Orientierung eines Streichholzes (also in welche Richtung der Kopf zeigt) ist irrelevant.  Eine Umformung, die diese Spielregeln erfüllt, wird in der Mathematik als Homöomorphismus bezeichnet.

Daraus folgt unmittelbar, dass…

…die Anzahl der Streichhölzer unverändert bleiben muss.
…die Anzahl der Knoten, also jener Stellen, wo sich zwei oder mehr Streichhölzer mit ihren Enden berühren, unverändert bleiben muss.
…die Anzahl der Knoten-Ordnungen unverändert bleiben muss. Knoten-Ordnung = Anzahl der Streichholzenden, die einander in einem Knoten berühren. Die Knoten-Ordnung darf auf einen anderen Knoten wechseln, ohne dabei die Spielregeln zu verletzen.

Beispiel 1:

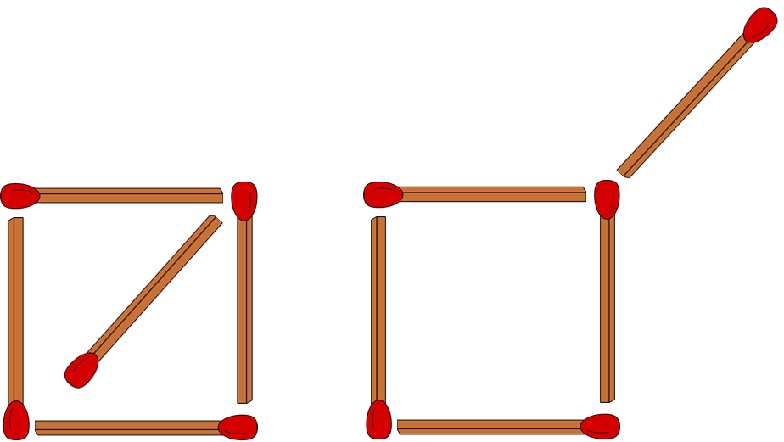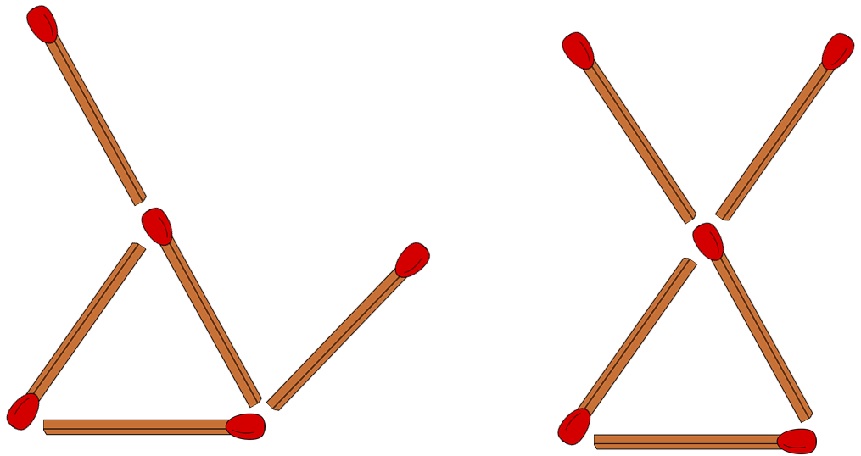Beispiel 2:

Anzahl an Streichhölzern	Anzahl topologisch unterschiedlicher Figuren
1
2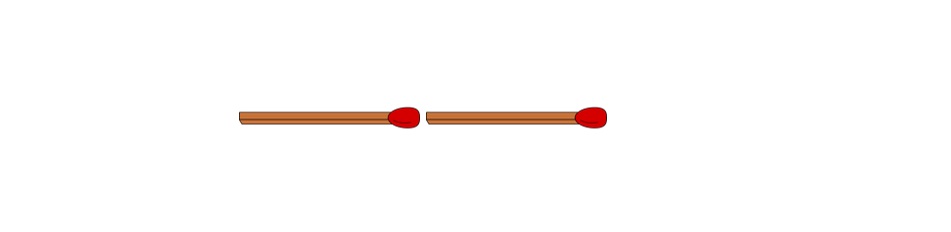
3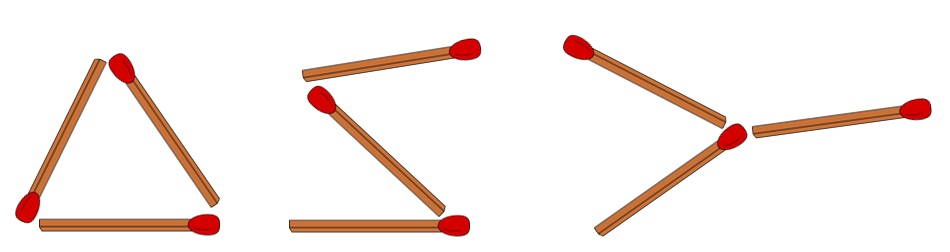

Verwendete Graphik: https://freesvg.org/match-stick

Februar ’20 – UNTERSTUFE
Lösungsvorschläge sind einzureichen bis spätestens 06.03.2020, 20:00 Uhr. Spielregeln beachten!
Unterstufenschüler/innen sind auch an der Oberstufen-Mathe-Challenge teilnahmeberechtigt.

Wie viele sich topologisch unterscheidende Figuren können (in einer Ebene, also auf dem Tisch) aus fünf Streichhölzern gebildet werden? Skizzen!

—————————–