The Mathemator Challenge – Spielregeln
The Mathemator Challenge – Spielregeln
- Der Lösungsvorschlag (Bilddatei, PDF- oder Word-Datei mit Namen und Klasse versehen an kom@gymgmunden.at) muss fristgerecht (Zeitstempel des EMails) eingereicht werden.
- Die Aufgabe muss ohne Technologieeinsatz gelöst und nachvollziehbar dokumentiert werden.
- Bei mehreren richtigen Lösungen folgt eine Reihung nach Zeitpunkt des Einlangens.
- Pro Runde darf nur ein Lösungsversuch eingereicht werden.
- Die Teilnehmerin/der Teilnehmer ist damit einverstanden, dass ihr/sein Lösungsvorschlag ggf. auf der Mathemator-Seite veröffentlicht wird.
- Der Gewinnerin/dem Gewinner winkt eine würdevolle Ehrung durch den Mathemator!
- Die Mathe-Challenge findet monatlich statt.
- Unterstufenschüler/innen sind auch an der Oberstufen-Mathe-Challenge teilnahmeberechtigt.
The Mathemator Challenge – Aufgaben
Jänner ’18 – UNTER- und OBERSTUFE
Lösungsvorschläge sind einzureichen bis spätestens 02.02.2018, 20:00 Uhr. Spielregeln beachten!
Zwei Personen (I und II, I beginnt) spielen ein Spiel. Das „Spielbrett“ ist rechteckig und besteht aus Quadraten (Spielfeldern). Das „Spielbrett“ ist mindestens drei Quadrate (Spielfelder) breit und lang.
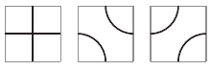
Die Spieler zeichnen abwechselnd eines der folgenden drei Muster in eines der Quadrate (Spielfelder) auf dem „Spielbrett“ ein:
Die nachstehenden Spielregeln sind einzuhalten:
- Spieler I muss bei seinem ersten Spielzug das Kreuzmuster in das linke, obere Quadrat (Spielfeld) des „Spielbretts“ einzeichnen.
- Daraufhin verlängert Spieler II mit einem der obigen Muster eine der beiden schwarzen Linien des Kreuzes.
- Jeder Spieler muss nun die schwarze Linie, die durch die ersten zwei Spielzüge entstanden ist, verlängern.
- Jene Person, die die schwarze Linie zum „Spielbrettrand“ führt, verliert das Spiel.
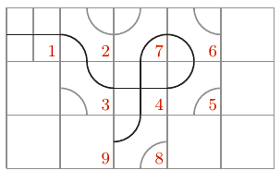
Beispiel: Die Ziffern geben die Reihenfolge der Spielzüge an. Das Spiel hier ist klarerweise noch nicht aus…
Aufgabe 1
Angenommen das „Spielbrett“ besteht aus einer ungeradzahligen Anzahl an Quadraten (Spielfeldern). Mit welcher „Gewinnstrategie“ kann einer der Spieler immer gewinnen? Welcher Spieler? Welche Strategie?
Aufgabe 2
Wie sieht die Situation bei einem „Spielbrett“ mit einer geradzahligen Anzahl an Quadraten (Spielfeldern) aus?
Viel Erfolg!
KOM
Lösungsvorschläge an: kom@gymgmunden.at
Idee und Abbildungen: http://www.deltami.edu.pl [15.01.2018]